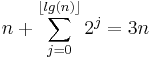Amortized analysis

In computer science, amortized analysis is a method of analyzing algorithms that considers the entire sequence of operations of the program. It allows for the establishment of a worst-case bound for the performance of an algorithm irrespective of the inputs by looking at all of the operations. At the heart of the method is the idea that while certain operations may be extremely costly in resources, they cannot occur at a high-enough frequency to weigh down the entire program because the number of less costly operations will far outnumber the costly ones in the long run, "paying back" the program over a number of iterations.^[1] It is particularly useful because it guarantees worst-case performance while accounting for the entire set of operations in an algorithm.

Contents 1 History 2 Method 3 Examples 4 Comparison to other methods 5 Common use 6 References

History

Amortized analysis initially emerged from a method called aggregate analysis, which is now subsumed by amortized analysis. However, the technique was first formally introduced by Robert Tarjan in his paper Amortized Computational Complexity, which addressed the need for a more useful form of analysis than the common probabilistic methods used. Amortization was initially used for very specific types of algorithms, particularly those involving binary trees and union operations. However, it is now ubiquitous and comes into play when analyzing many other algorithms as well.^[1]

Method

The method requires knowledge of which series of operations are possible. This is most commonly the case with data structures, which have state that persists between operations. The basic idea is that a worst case operation can alter the state in such a way that the worst case cannot occur again for a long time, thus "amortizing" its cost.

There are generally three methods for performing amortized analysis: the aggregate method, the accounting method, and the potential method. All of these give the same answers, and their usage difference is primarily circumstantial and due to individual preference.^[2]

• Aggregate analysis determines the upper bound T(n) on the total cost of a sequence of n operations, then calculates the average cost to be T(n) / n.^[2]
• The accounting method determines the individual cost of each operation, combining its immediate execution time and its influence on the running time of future operations. Usually, many short-running operations accumulate a "debt" of unfavorable state in small increments, while rare long-running operations decrease it drastically.^[2]
• The potential method is like the accounting method, but overcharges operations early to compensate for undercharges later.^[2]

Examples

As a simple example, in a specific implementation of the dynamic array, we double the size of the array each time it fills up. Because of this, array reallocation may be required, and in the worst case an insertion may require O(n). However, a sequence of n insertions can always be done in O(n) time, because the rest of the insertions are done in constant time, so n insertions can be completed in O(n) time. The amortized time per operation is therefore O(n) / n = O(1).

Another way to see this is to think of a sequence of n operations. There are 2 possible operations: a regular insertion which requires a constant c time to perform (assume c = 1), and an array doubling which requires O(j) time (where j<n and is the size of the array at the time of the doubling). Clearly the time to perform these operations is less than the time needed to perform n regular insertions in addition to the number of array doublings that would have taken place in the original sequence of n operations. There are only as many array doublings in the sequence as there are powers of 2 between 0 and n ( lg(n) ). Therefore the cost of a sequence of n operations is strictly less than the below expression:^[3]

The amortized time per operation is the worst-case time bound on a series of n operations divided by n. The amortized time per operation is therefore O(3n) / n = O(n) / n = O(1).

Comparison to other methods

Notice that average-case analysis and probabilistic analysis of probabilistic algorithms are not the same thing as amortized analysis. In average-case analysis, we are averaging over all possible inputs; in probabilistic analysis of probabilistic algorithms, we are averaging over all possible random choices; in amortized analysis, we are averaging over a sequence of operations. Amortized analysis assumes worst-case input and typically does not allow random choices.

An average-case analysis for an algorithm is problematic because the user is dependent on the fact that a given set of inputs will not trigger the worst case scenario. A worst-case analysis has the property of often returning an overly pessimistic performance for a given algorithm when the probability of a worst-case operation occurring multiple times in a sequence is 0 for certain programs.

Common use

• In common usage, an "amortized algorithm" is one that an amortized analysis has shown to perform well.
• Online algorithms commonly use amortized analysis.

References

• Allan Borodin and Ran El-Yaniv (1998). Online Computation and Competitive Analysis. Cambridge University Press. pp. 20,141. http://www.cs.technion.ac.il/~rani/book.html.